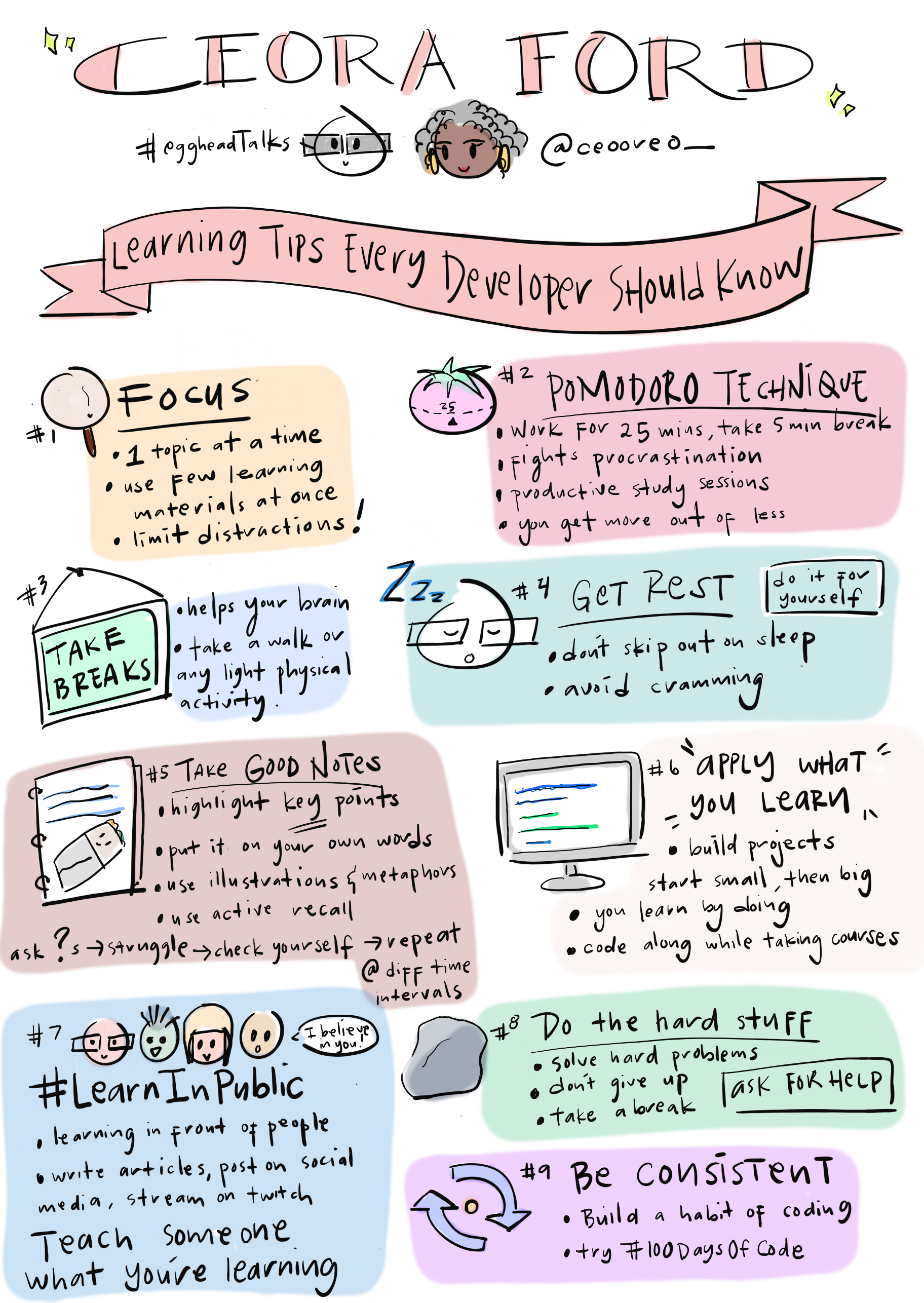
Learning Tips Every Developer Should Know
This talk is going to point out some of the biggest pitfalls you need to avoid. It'll also highlight steps you can take to successfully learn any coding language or skill.
Transcript
Ceora Ford: [0:00] Hi, everyone. Thanks so much for tuning in. My name is Ceora, and I'm going to be talking about learning tips that every developer should know.
[0:09] A little bit about me. I'm a software engineer based in Philadelphia. I'm also a learner advocate at egghead.io. I teach at Kode With Klossy and BSD Education in the summer, and I'm currently learning Python and cloud engineering. I've also [laughs] failed at learning plenty of times in the past.
[0:28] Why am I someone you should listen to when it comes to this topic? Well, like I said earlier, [laughs] I failed at learning plenty of times in the past. I even wrote an article about the five mistakes I made my first year learning how to code.
[0:40] Because of that, I've done lots of research on this very topic. I've watched videos. I've read articles. I've also even taken a course on learning how to learn, so what I'm emphasizing right now will be based on the combination of my own research and personal experiences.
[0:57] Throughout this presentation, you'll hear me reference a lot of talks and articles and things like that that I've read or listened to. I'm going to be putting together an article that's going to feature the courses I've taken, the videos I've watched, the talks I listened to, so that you can look at them too, if you want, at your leisure.
[1:15] Why is this relevant to you? Why should you care about learning, about knowing how to learn? Our industry is ever-changing, so there's always something new to learn. You'll find that, when you know how to learn, you'll gain a better foundational knowledge, which is important, especially for those who are just starting out.
[1:36] You'll also waste less time, and you'll retain information for the long term. You'll also become a better teacher. This is important, because teaching is something that a lot of us eventually have to do in this industry.
[1:54] If you're more interested in knowing how to become a better teacher, I highly recommend watching Ali Spittel's talk about how to teach code, but in short, what I'm going to say is that being a good learner makes you a better teacher. Those are some of the reasons why it's so important to know how to learn.
[2:15] Let's get right into it. Tip number one is to focus. Focus how? That's such a broad term. When I say focus, I mean in three main ways. The first way is to focus on one topic at a time. There are so many different things to learn in tech. It can be easy to try to focus on learning different languages and technologies all at the same time.
[2:40] This is definitely something I did, and I found that I became a jack of all trades and a master of none. I was never able to gain a substantial knowledge of any coding language. This is why something I discourage people from doing. If you would like to have a more in-depth knowledge of a certain topic or language, try to focus on one language at a time.
[3:05] Try to focus on a few learning materials at a time. That's the second way you want to focus. Don't bog yourself down with trying to take a bunch of different courses at once, trying to read a bunch of books at once. This can ultimately lead to, again, not having a substantial grasp of the information. This is, [laughs] again, something that I did. Try to focus on a few learning materials at once.
[3:36] If you can, try to learn in a distraction-free zone. This is nearly impossible for most of us, [laughs] especially now, but try to limit distractions as much as possible.
[3:49] For me, that means turning the notifications off on my phone. Sometimes I have to put my phone across the room. I also like to listen to white noise playlists on YouTube, which, again, I'll be listing in my article of resources for anyone that's interested.
[4:08] Tip number two is to use the Pomodoro Technique. This is one of my favorite learning techniques out there. What is the Pomodoro Technique? It's the workflow of working or studying for 25 minutes and taking a 5-minute break, working for 25 minutes, taking a 5-minute break.
[4:29] What makes the Pomodoro Technique so special? It helps us to tackle procrastination. Having a 5-minute break at the end of your 25-minute work session tricks your brain into looking forward to a reward so that, while you're working, your brain is more focused on the reward or the break to come.
[4:51] This helps us to hijack procrastination, which can be a huge barrier for some of us [laughs] when we're trying to get things done. Using the Pomodoro Technique also helps us to create focused and productive study sessions. You'll find that you can get more out of less.
[5:12] What do I mean when I say this? Because you'll have more focused study sessions, you'll be gaining more in-depth knowledge, and you'll be doing this in less time. You'll be getting more out of less, which is important now since most of us are super busy.
[5:31] Tip number three is to take breaks. This goes right in tandem with the Pomodoro Technique. Even if you decide not to use the Pomodoro Technique, it's still important to have breaks. Taking short breaks during your study sessions can help take your mind off of the information that you're learning. Doing this can help your brain to do a lot of work in the background.
[5:55] I also suggest adding some light physical activity into your breaks. I don't mean hardcore exercising unless that's something that you're into, but more like taking short walks, or even just getting up from your desk and walking around your house or your apartment, and maybe taking a light stretch. Doing this can help your brain to synthesize information in the background.
[6:23] Think about times when you've taken a walk or taken a shower, and you came up with a solution to a problem. This is how that works, so make sure to take your breaks. It does your brain a lot of favors.
[6:37] Tip number four is to get rest. Now, I've noticed that a lot of people tend to skip out on sleep in order to get more studying done, especially when they're starting off their coding journey, but this is not such a good idea. If you can, try not to skip out on sleep to get more studying done. Our brains do so much work in the background when we're sleeping, again, like when we take breaks.
[7:01] Even more so, since sleep is a long break that we definitely need, try to avoid cramming if you can. I'm not going to give you any hard and fast rules as far as how much sleep you should get. Get enough rest for you. Do whatever works for you as far as this is concerned. Don't miss out on sleep.
[7:24] Tip number five is to take good notes. As a learner advocate at egghead, I cannot skip out on this one. Here's some of my tips for taking good notes. Here are some things that worked for me.
[7:36] Number one, is to only highlight key information, try to discern what the key points are and whatever information you're going over and highlight those, focus on those, draw your attention to those points.
[7:49] Number two, is to put information in your own words. To put information in your own words, meaning that you have to truly understand what you're learning, which can help you to, again, discern what parts of the information you don't know so well and what parts you need to work on. Definitely try not to copy and paste while you're reading. Try to put in your own words.
[8:10] Number three, is I like to handwrite my notes. Not everyone does, but I find that I retain the information better when I handwrite them. Do what works for you, but for me, handwritten notes yield the best results.
[8:24] Number four, is probably my most favorite tip. Lately, it's been the tip that I've been using the most, and that is using illustrations and metaphors. If you're more interested in hearing about this more in-depth, I highly recommend watching Maggie Appleton's talk about visual metaphors. She gave it at Women of React. Again, I'll be listing that in my article of resources.
[8:51] Using illustrations is great because it helps you to bring some of the abstract concepts that we're learning and that we have to master. It helps you to bring them down to human level. You can relate them to things that you're familiar with, which will help you to learn information even better.
[9:10] Number five, is something that I don't hear as much, but I like to use active recall when I take my notes. What is active recall? Well, it's literally the act of recalling information. Think about an exam, think about a question-and-answer format. You read the question, and it forces you to recall the information.
[9:32] I like to write my notes in this question-and-answer format because it helps me, especially when I'm reviewing information to automatically see where I need to improve if I can't answer the question, and it's obviously something that I need to do extra work with.
[9:47] Number six, is to do what works for you. If you're a visual learner, make illustrations, make drawings, do mind maps. If you're an audio learner, watch videos. Do whatever works for you. Find your learning style and work with that.
[10:04] Here are some pictures of my notes. On the left, you'll see some notes that I took using the active recall method, the question-and-answer format, and then on the right, you'll see an illustration I did of a burrito. It's supposed to illustrate how slicing lists works in Python.
[10:22] I imagine sharing a burrito with my friend and cutting it up into pieces. That's how slicing lists works in my brain, anyway.
[10:33] Tip number six is to apply what you learn. How do you apply what you learn? By building projects, big or small. Sometimes building a project can seem intimidating, so start small and build on it over time. This is something I love doing because it helps you to see how your knowledge is growing.
[10:53] If you start off with a simple calculator and build it out to something that has much more functionality, or even a small game, something I love doing. Also, try to code along with whatever courses or videos you're watching. It helps you to take your learning to the active level as opposed to passively learning.
[11:14] Again, you'll retain information much more. Learning by doing is such a strong learning technique even if you're curious about a certain behavior, or if you're curious to see if a certain solution will work, test it out, type out the code, do it. You'll grasp the information so much better.
[11:35] Tip number seven, is to learn in public. It's cool that Sean is giving his talk right after mine because he is the king of learning in public. What is learning in public? Basically, to boil it down in its most basic form, learning in public is learning in front of other people, teaching other people what you're learning.
[11:59] A great way to do this, there are several great ways to do this. My favorite are to write articles. You can write articles on dev.to. You can stream yourself building projects on Twitch. You can even share what you're learning on social media, sharing on Twitter through a 100 Days of Code.
[12:15] Even if you're not someone who's a fan of sharing information online, you can even share what you're learning with friends and family. You can even share what you're learning with inanimate objects. You can use the rubber ducking method to explain what you're learning. Teach someone or something what you're learning, and you'll be learning in public.
[12:36] Tip number eight, is to do the hard stuff. This was something that I was extremely horrible at. I fell into the awful cycle of running into something that was difficult, giving up and running away, and then coming back and forgetting everything that I learned. This is a cycle that I fell into over and over again. Don't be like me, do the hard stuff. Try to solve hard problems.
[13:02] If you're still struggling, take a break, whether it be for five minutes or for the whole day. Then, after your break, try to solve the problem again. If you're still struggling, ask for help. Go to Twitter, join some beginner-friendly or whatever level you are friendly communities out there. There are plenty that have people who are definitely willing to help you out.
[13:26] You can even post on Stack Overflow if you like adding new Stack Overflow as much, but it's definitely an option for getting help.
[13:35] Tip number nine, is to be consistent. Again, this was something that I was not good at, but there's huge value in practicing consistently. You don't have to practice every day. Some of us can't do that. We can't fit that into our schedule, which is totally fine. Build the habit of coding.
[13:54] Try to do it three days a week if you can, four days a week, whatever works for you and your schedule. If you can, try the 100 Days of Code challenge. It helps you to become accountable to a huge supportive community. It also helps you to build a habit of coding every day. We're pretty much done with our presentation.
[14:17] To summarize it all here, the key things that you need to remember. Focus, use the Pomodoro Technique if you would like. Try to make sure to take breaks and get rest. Take good notes. Apply what you learn by building projects. Learn in public. Do the hard stuff and be consistent.
[14:36] That's all from me. Thank you so much for watching. I appreciate it. If you have any questions, any feedback, or if you want to chat, reach out to me on Twitter @ceeoreo_. You can also visit my website ceoraford.com. You can find some of my articles on dev.to. Thank you so much for watching.